Grades are Not Normal

Sometimes you just feel like squashing normals:

Logit Normal
The logit normal is the continuous distribution that results from applying a special "squashing" function to a Normally distributed random variable. The squashing function maps all values the normal could take on onto the range 0 to 1. If $X \sim \text{LogitNormal}(\mu, \sigma^2)$ it has: \begin{align*} \text{PDF:}&& &f_X(x) = \begin{cases} \frac{1}{\sigma(\sqrt{2\pi})x(1 - x)}e^{-\frac{(\text{logit}(x) - \mu)^2}{2\sigma^2}} & \text{if } 0 < x < 1\\ 0 & \text{otherwise} \end{cases} \\ \text{CDF:} && &F_X(x) = \Phi\Big(\frac{\text{logit}(x) - \mu}{\sigma}\Big)\\ \text{Where:} && &\text{logit}(x) = \text{log}\Big(\frac{x}{1-x}\Big) \end{align*}

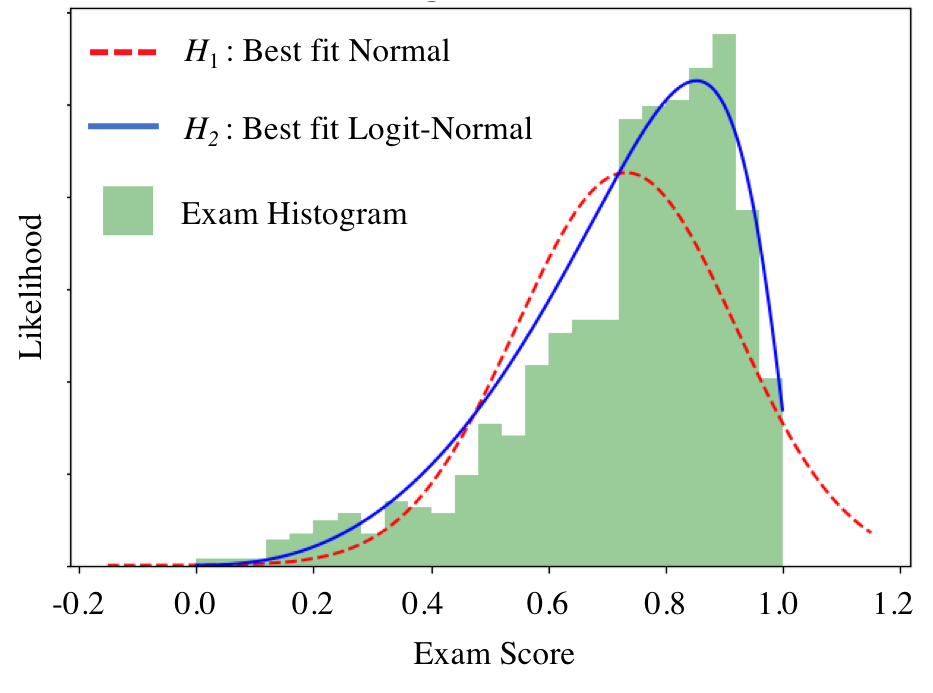
A new theory shows that the Logit Normal better fits exam score distributions than the traditionally used Normal. Let's test it out! We have some set of exam scores for a test with min possible score 0 and max possible score 1, and we are trying to decide between two hypotheses:

$H_1$: our grade scores are distributed according to $X\sim \text{Normal}(\mu = 0.7, \sigma^2 = 0.2^2)$.
$H_2$: our grade scores are distributed according to $X\sim \text{LogitNormal}(\mu = 1.0, \sigma^2 = 0.9^2)$.

Under the normal assumption, $H_1$, what is $P(0.9 < X < 1.0)$? Provide a numerical answer to two decimal places.

$$P(0.9 < X < 1.0) = \Phi\left(\frac{1.0 - 0.7}{0.2}\right) - \Phi\left(\frac{0.9 - 0.7}{0.2}\right) = \Phi(1.5) - \Phi(1.0) = 0.9332 - 0.8413 = 0.09$$

Under the logit-normal assumption, $H_2$, what is $P(0.9 < X < 1.0)$?

$$F_X(1.0) - F_X(0.9) = \Phi\Big(\frac{\text{logit}(1.0) - 1.0}{0.9}\Big) - \Phi\Big(\frac{\text{logit}(0.9) - 1.0}{0.9}\Big)$$ Which we can solve for numerically: $$\Phi\Big(\frac{\text{logit}(1.0) - 1.0}{0.9}\Big) - \Phi\Big(\frac{\text{logit}(0.9) - 1.0}{0.9}\Big) = 1 - \Phi(1.33) \approx 0.91$$

Under the normal assumption, $H_1$, what is the maximum value that $X$ can take on?

$$\infty$$

Before observing any test scores, you assume that (a) one of your two hypotheses is correct and (b) that initially, each hypothesis is equally likely to be correct, $P(H_1)=P(H_2)=\frac{1}{2}$. You then observe a single test score, $X = 0.9$. What is your updated probability that the Logit-Normal hypothesis is correct?

\begin{align*} P(H_2|X = 0.9) &= \frac{f(X = 0.9|H_2)P(H_2)}{f(X = 0.9|H_2)P(H_2) + f(X = 0.9|H_1)P(H_1)}\\ &= \frac{f(X = 0.9|H_2)}{f(X = 0.9|H_2) + f(X = 0.9|H_1)}\\ &= \frac{\frac{1}{\sigma(\sqrt{2\pi})0.9*(1 - 0.9)}e^{-\frac{(\text{logit}(0.9) - 1.0)^2}{2*0.9^2}}}{\frac{1}{\sigma(\sqrt{2\pi})0.9*(1 - 0.9)}e^{-\frac{(\text{logit}(0.9) - 1.0)^2}{2*0.9^2}} + \frac{1}{0.2\sqrt{2\pi}}e^{-\frac{(0.9 - 0.7)^2}{2*0.2^2}}} \end{align*}