$\DeclareMathOperator{\p}{P}$ $\DeclareMathOperator{\P}{P}$ $\DeclareMathOperator{\c}{^C}$ $\DeclareMathOperator{\or}{ or}$ $\DeclareMathOperator{\and}{ and}$ $\DeclareMathOperator{\var}{Var}$ $\DeclareMathOperator{\Var}{Var}$ $\DeclareMathOperator{\Std}{Std}$ $\DeclareMathOperator{\E}{E}$ $\DeclareMathOperator{\std}{Std}$ $\DeclareMathOperator{\Ber}{Bern}$ $\DeclareMathOperator{\Bin}{Bin}$ $\DeclareMathOperator{\Poi}{Poi}$ $\DeclareMathOperator{\Uni}{Uni}$ $\DeclareMathOperator{\Geo}{Geo}$ $\DeclareMathOperator{\NegBin}{NegBin}$ $\DeclareMathOperator{\Beta}{Beta}$ $\DeclareMathOperator{\Exp}{Exp}$ $\DeclareMathOperator{\N}{N}$ $\DeclareMathOperator{\R}{\mathbb{R}}$ $\DeclareMathOperator*{\argmax}{arg\,max}$ $\newcommand{\d}{\, d}$

Winning the Series

The Golden State Warriors are the basketball team for the Bay Area. The Warriors are going to play the Bucks (another professional basketball team) in a best of 7 series during the next NBA finals. They will win the series if you win at least 4 games. What is the probability that the warriors win the series? Each game is independent. Each game, the warriors have a 0.55 probability of winning.

This problem is equivalent to: Flip a biased coin 7 times (with a $p=0.55$ probability of getting a heads). What is the probability of at least 4 heads?

Note: without loss of generality you could imagine that the two teams always play all 7 games, regardless of the outcome. Technically they stop playing after one team has achieved 4 wins, because the outcomes of the games no longer impact who wins. However, you could imagine that they continue.

What is the probability that the warriors win the series? Leave your answer to 3 decimal places

A critical step is to define a random variable and to recognize it is a Binomial. Let $X$ be the number of games won. Since each game is independent, $X \sim \Bin(n=7, p =0.55)$. The question is asking: $\P(X \geq 4)$?

To answer this question, first recognize that: \begin{aligned}\P(X \geq 4) = &\P(X = 4) + \P(X = 5) \\ &+ \P(X = 6) + \P(X = 7)\end{aligned} This is because the question is asking the probability of the "or" of each of the events on the right hand side of the equals sign. Since each of these events; $X=4$, $X=5$, etc are mutually exclusive, the probability of the "or" is simply the sum of the probabilities.

\begin{aligned} \P(X \geq 4) &= \P(X = 4) + \P(X = 5) \\ &+ \P(X = 6) + \P(X = 7) \\ &= \sum_{i=4}^7 P(X = i) \end{aligned}

Each of these probabilities are PMF questions:

\begin{aligned} \P(X \geq 4) &= \sum_{i=4}^7 P(X = i) \\ &= \sum_{i=4}^7 {n \choose i} p^i (1-p)^{n-i} \\ &= \sum_{i=4}^7 {7 \choose i} 0.55^i \cdot 0.45^{7-i} \end{aligned}

Here is that equation graphically. It represents the sum of these columns in the PMF:

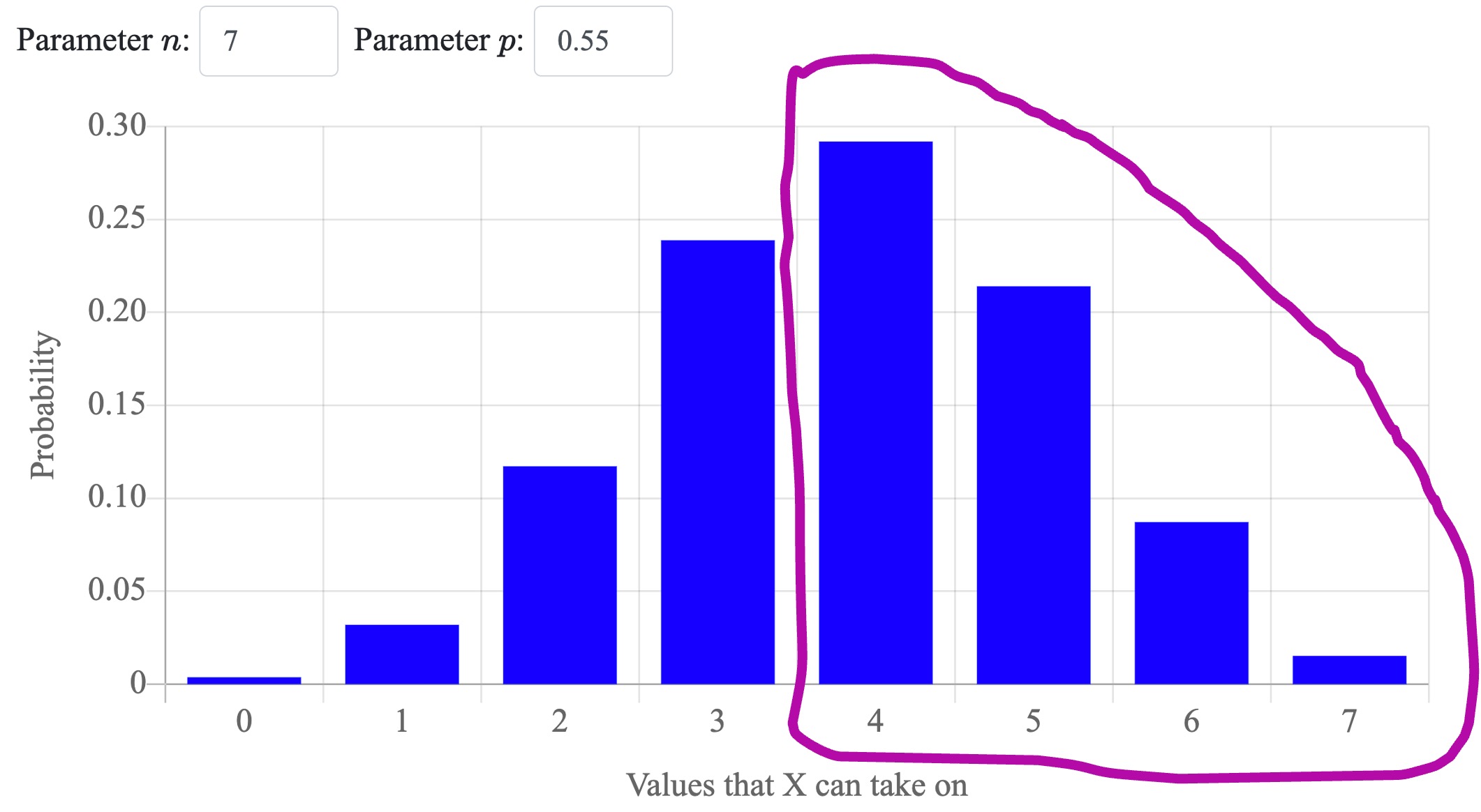
At this point we have an equation that we can compute in order to find the answer. But how should we compute it? We could do it by hand! Or using a calculator. Or, we can use python, and specifically the scipy package: 

from scipy import stats

pr = 0
# calculate the sum
for i in range(4, 8): 
   # this for loop gives i in [4,5,6,7] 
   pr_i = stats.binom.pmf(i, n = 7, p = 0.55)
   pr += pr_i

print(f'P(X >= 4) = {pr}')

Which produces the correct answer:

P(X >= 4) = 0.6082877968750001

Buggy Solution

A good reason to study this problem is because of this common misconception for how to compute $P(X \geq 4)$. It is worth understanding why it is wrong.

Incorrectly trying to recreate the binomial

Similar to how we defined a binomial distribution PMF equation (see: Many Coin Flips) we can construct outcomes of the seven game series where the warriors win.

We are going to choose 4 slots where the Warriors win, and we don't care about the rest. They could either be wins or losses. Out of 7 games, select 4 where the Warriors win. There are $7 \choose 4$ ways to do so. The probability of each particular selection of four games to win is $p^4$ because we need them to win those four games, and we don't care about the rest. As such the probability is:

\begin{aligned} P(X \geq 4) = {7 \choose 4} p^4 \end{aligned}

This idea seems good, but it doesn't work. First of all, we can recognize that there is a problem by considering the outcome if we set $p = 1.0$. In this case $P(X \geq 4) = {7 \choose 4} p^4 ={7 \choose 4} 1 ^4 = 35$. Clearly 35 is an invalid probability (which is much greater than 1). As such this can't be the right answer.

But what is wrong with this approach? Lets enumerate the 35 different outcomes that they are considering. Let B = we don't know who wins. Let W = the warriors win. Here each outcome is the assignment to each of the 7 games in the series:

    (B, B, B, W, W, W, W)
    (B, B, W, B, W, W, W)
    (B, B, W, W, B, W, W)
    (B, B, W, W, W, B, W)
    (B, B, W, W, W, W, B)
    (B, W, B, B, W, W, W)
    (B, W, B, W, B, W, W)
    (B, W, B, W, W, B, W)
    (B, W, B, W, W, W, B)
    (B, W, W, B, B, W, W)
    (B, W, W, B, W, B, W)
    (B, W, W, B, W, W, B)
    (B, W, W, W, B, B, W)
    (B, W, W, W, B, W, B)
    (B, W, W, W, W, B, B)
    (W, B, B, B, W, W, W)
    (W, B, B, W, B, W, W)
    (W, B, B, W, W, B, W)
    (W, B, B, W, W, W, B)
    (W, B, W, B, B, W, W)
    (W, B, W, B, W, B, W)
    (W, B, W, B, W, W, B)
    (W, B, W, W, B, B, W)
    (W, B, W, W, B, W, B)
    (W, B, W, W, W, B, B)
    (W, W, B, B, B, W, W)
    (W, W, B, B, W, B, W)
    (W, W, B, B, W, W, B)
    (W, W, B, W, B, B, W)
    (W, W, B, W, B, W, B)
    (W, W, B, W, W, B, B)
    (W, W, W, B, B, B, W)
    (W, W, W, B, B, W, B)
    (W, W, W, B, W, B, B)
    (W, W, W, W, B, B, B)

It is in fact the case that the probability of any of these 35 outcomes is $p^4$. For example: (W, W, W, W, B, B, B). The warriors need to win the first 4 independent games: $p^4$. Then there are three events where either team could win. The probability of "B", that either team could win, is 1. That makes sense. Either the warriors win or the other team wins. As such our probability of any given outcome, aka row in the set of outcomes above, is: $p^4 \cdot 1 ^3 = p^4$

The bug here is that these outcomes are not mutually exclusive, yet the answer treats them as such. In the many coin flips example, we constructed outcomes in the format (T, T, T, H, H, T, H). These outcomes are in fact mutually exclusive. Its not possible for two distinct lists of outcomes to simultaneously exist. On the other hand in the version where "B" stands for either team could win, the outcomes do have overlap. For example consider the two rows from the examples above:

    (B, W, W, W, B, B, W)
    (B, W, W, W, B, W, B)

These could both occur (and hence are not mutually exclusive). For example if the warriors win all 7 games! Or the warriors win all games except for games 1 and 5. Both events are satisfied. Because the events are not mutually exclusive, if we want the probability of the "or" of each of these events we can not just sum the probabilities of each of the events (and that is exactly what $P(X \geq 4) = {7 \choose 4} p^4$ implies. Instead you would need to use inclusion exclusion for the or of 35 events (yikes!). Alternatively see the answer we propose above.