Conditional Probability
In English, a conditional probability states "what is the chance of an event $E$ happening given that I have already observed some other event $F$". It is a critical idea in machine learning and probability because it allows us to update our probabilities in the face of new evidence.
When you condition on an event happening you are entering the universe where that event has taken place. Formally, once you condition on $F$ the only outcomes that are now possible are the ones which are consistent with $F$. In other words your sample space will now be reduced to $F$. As an aside, in the universe where $F$ has taken place, all rules of probability still hold!
The probability of E given that (aka conditioned on) event F already happened: $$ \p(E |F) = \frac{\p(E \and F)}{\p(F)} $$
Let's use a visualization to get an intuition for why the conditional probability formula is true. Again consider events $E$ and $F$ which have outcomes that are subsets of a sample space with 50 equally likely outcomes, each one drawn as a hexagon:
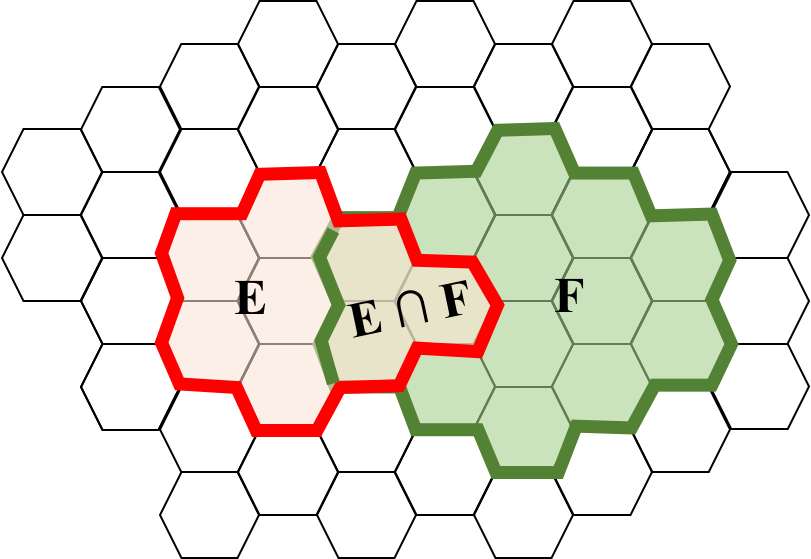
Conditioning on $F$ means that we have entered the world where $F$ has happened (and $F$, which has 14 equally likely outcomes, has become our new sample space). Given that event $F$ has occurred, the conditional probability that event $E$ occurs is the subset of the outcomes of E that are consistent with $F$. In this case we can visually see that those are the three outcomes in $E \and F$. Thus we have the: $$ \p(E |F) = \frac{\p(E \and F)}{\p(F)} = \frac{3/50}{14/50} = \frac{3}{14} \approx 0.21 $$ Even though the visual example (with equally likely outcome spaces) is useful for gaining intuition, conditional probability applies regardless of whether the sample space has equally likely outcomes!
Conditional Probability Example
Let's use a real world example to better understand conditional probability: movie recommendation. Imagine a streaming service like Netflix wants to figure out the probability that a user will watch a movie $E$ (for example, Life is Beautiful), based on knowing that they watched a different movie $F$ (say Amélie). To start lets answer the simpler question, what is the probability that a user watches the movie Life is Beautiful, $E$? We can solve this problem using the definition of probability and a dataset of movie watching [1]: $$ \begin{align} \p(E) &= \lim_{n \rightarrow \infty} \frac{\text{count}(E)}{n} \approx \frac{\text{# people who watched movie $E$}}{\text{# people on Netflix}} \\ &= \frac{1,234,231}{50,923,123} \approx 0.02 \end{align} $$ In fact we can do this for many movies $E$:
 $\p(E) = 0.02$
$\p(E) = 0.02$ $\p(E) = 0.01$
$\p(E) = 0.01$ $\p(E) = 0.05$
$\p(E) = 0.05$ $\p(E) = 0.09$
$\p(E) = 0.09$ $\p(E) = 0.03$
$\p(E) = 0.03$Now for a more interesting question. What is the probability that a user will watch the movie Life is Beautiful ($E$), given they watched Amelie ($F$)? We can use the definition of conditional probability. $$ \begin{align} \p(E|F) &= \frac{\p(E \and F)}{\p(F)} && \text{Def of Cond Prob}\\ &\approx \frac{ (\text{# who watched $E \and F$}) / (\text{# of people on Netflix}) }{ (\text{# who watched movie $F$}) / (\text{# people on Netflix}) } && \text{Def of Prob} \\ &\approx \frac{\text{# of people who watched both $E \and F$}}{\text{# of people who watched movie $F$}} && \text{Simplifying} \end{align} $$ If we let $F$ be the event that someone watches the movie Amélie, we can now calculate $\p(E|F)$, the conditional probability that someone watches movie $E$:
 $\p(E|F) = 0.09$
$\p(E|F) = 0.09$ $\p(E|F) = 0.03$
$\p(E|F) = 0.03$ $\p(E|F) = 0.05$
$\p(E|F) = 0.05$ $\p(E|F) = 0.02$
$\p(E|F) = 0.02$ $\p(E|F)$ = 1.00
$\p(E|F)$ = 1.00Why do some probabilities go up, some probabilities go down, and some probabilities are unchanged after we observe that the person has watched Amelie ($F$)? If you know someone watched Amelie, they are more likely to watch Life is Beautiful, and less likely to watch Star Wars. We have new information on the person!
The Conditional Paradigm
When you condition on an event you enter the universe where that event has taken place. In that new universe all the laws of probability still hold. Thus, as long as you condition consistently on the same event, every one of the tools we have learned still apply. Let’s look at a few of our old friends when we condition consistently on an event (in this case $G$):
| Name of Rule | Original Rule | Rule Conditioned on $G$ |
|---|---|---|
| Axiom of probability 1 | $0 ≤ \p(E) ≤ 1$ | $0 ≤ \p(E|G) ≤ 1$ |
| Axiom of probability 2 | $\p(S) = 1$ | $\p(S | G) = 1$ |
| Axiom of probability 3 | $\p(E \or F) = \p(E) + \p(F)$ for mutually exclusive events |
$\p(E \or F | G) = \p(E | G) + \p(F | G)$ for mutually exclusive events |
| Identity 1 | $\p(E\c) = 1 - \p(E)$ | $\p(E\c | G) = 1 - \p(E |G)$ |
Conditioning on Multiple Events
The conditional paradigm also applies to the definition of conditional probability! Again if we consistently condition on some event $G$ occurring, the rule still holds:
$$
\p(E |F, G) = \frac{\p(E \and F | G)}{\p(F | G)}
$$
The term $\p(E | F, G)$ is new notation for conditioning on multiple events. You should read that term as "The probability of E occurring, given that both F and G have occurred". This equation states that the definition for conditional probability of $E | F$ still applies in the universe where $G$ has occurred. Do you think that $\p(E |F, G)$ should be equal to $\p(E |F)$? The answer is: sometimes yes and sometimes no.