$\DeclareMathOperator{\p}{P}$ $\DeclareMathOperator{\P}{P}$ $\DeclareMathOperator{\c}{^C}$ $\DeclareMathOperator{\or}{ or}$ $\DeclareMathOperator{\and}{ and}$ $\DeclareMathOperator{\var}{Var}$ $\DeclareMathOperator{\Var}{Var}$ $\DeclareMathOperator{\Std}{Std}$ $\DeclareMathOperator{\E}{E}$ $\DeclareMathOperator{\std}{Std}$ $\DeclareMathOperator{\Ber}{Bern}$ $\DeclareMathOperator{\Bin}{Bin}$ $\DeclareMathOperator{\Poi}{Poi}$ $\DeclareMathOperator{\Uni}{Uni}$ $\DeclareMathOperator{\Geo}{Geo}$ $\DeclareMathOperator{\NegBin}{NegBin}$ $\DeclareMathOperator{\Beta}{Beta}$ $\DeclareMathOperator{\Exp}{Exp}$ $\DeclareMathOperator{\N}{N}$ $\DeclareMathOperator{\R}{\mathbb{R}}$ $\DeclareMathOperator*{\argmax}{arg\,max}$ $\newcommand{\d}{\, d}$

Probability of or

The equation for calculating the probability of either event E or event F happening, written $\p(E \or F)$ or equivalently as $\p(E ∪ F)$, is deeply analogous to counting the size of two sets. As in counting, the equation that you can use depends on whether or not the events are "mutually exclusive". If events are mutually exclusive, it is very straightforward to calculate the probability of either event happening. Otherwise, you need the more complex "inclusion exclusion" formula.

Mutually exclusive events

Two events: $E$, $F$ are considered to be mutually exclusive (in set notation $E ∩ F = ∅$) if there are no outcomes that are in both events (recall that an event is a set of outcomes which is a subset of the sample space). In English, mutually exclusive means that two events can't both happen.

Mutual exclusion can be visualized. Consider the following visual sample space where each outcome is a hexagon. The set of all the fifty hexagons is the full sample space:


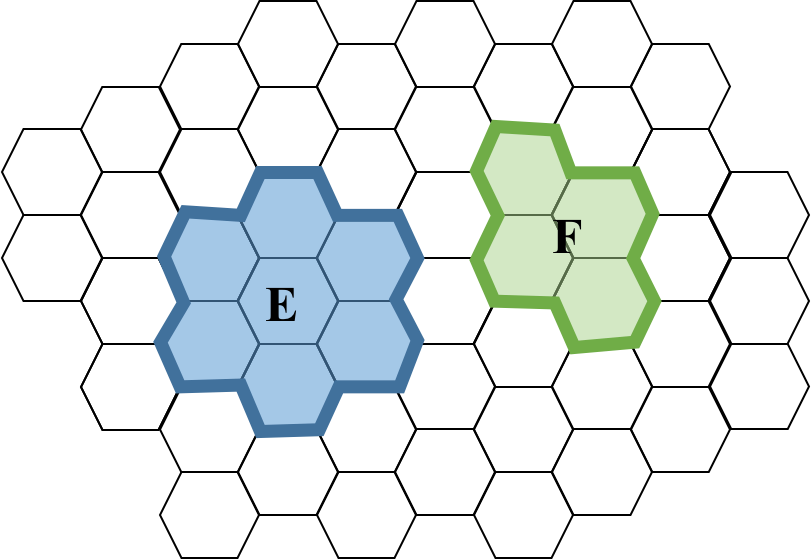
Example of two events: $E$, $F$, which are mutually exclusive.

Both events $E$ and $F$ are subsets of the same sample space. Visually, we can note that the two sets do not overlap. They are mutually exclusive: there is no outcome that is in both sets.

Or with Mutually Exclusive Events

Definition: Probability of or for mututally exclusive events

If two events: $E$, $F$ are mutually exclusive then the probability of $E$ or $F$ occurring is: $$ \p(E \or F) = \p(E) + \p(F) $$

This property applies regardless of how you calculate the probability of $E$ or $F$. Moreover, the idea extends to more than two events. Lets say you have $n$ events $E_1, E_2, \dots E_n$ where each event is mutually exclusive of one another (in other words, no outcome is in more than one event). Then: $$ \p(E_1 \or E_2 \or \dots \or E_n) = \p(E_1) + \p(E_2) + \dots + \p(E_n) = \sum_{i=1}^n \p(E_i) $$

You may have noticed that this is one of the axioms of probability. Though it might seem intuitive, it is one of three rules that we accept without proof.

Caution: Mutual exclusion only makes it easier to calculate the probability of $E \or F$, not other ways of combining events, such as $E \and F$.

At this point we know how to compute the probability of the "or" of events if and only if they have the mutual exclusion property. What if they don't?

Or with Non-Mutually Exclusive Events

Unfortunately, not all events are mutually exclusive. If you want to calculate $\p(E \or F)$ where the events $E$ and F are not mutually exclusive you can not simply add the probabilities. As a simple sanity check, consider the event $E$: getting heads on a coin flip, where $\p(E) = 0.5$. Now imagine the sample space $S$, getting either a heads or a tails on a coin flip. These events are not mutually exclusive (the outcome heads is in both). If you incorrectly assumed they were mutually exclusive and tried to calculate $\p(E \or S)$ you would get this buggy derivation:

Buggy derivation: Incorrectly assuming mutual exclusion

Calculate the probability of $E$, getting an even number on a dice role (2, 4 or 6), or $F$, getting three or less (1, 2, 3) on the same dice role. $$ \begin{align} \p(E \or F) &= \p(E) + \p(F) && \text{Incorrectly assumes mutual exclusion} \\ &= 0.5 + 0.5 && \text{substitute the probabilities of $E$ and $S$} \\ &= 1.0 && \text{uh oh!} \end{align} $$

The probability can't be one since the outcome 5 is neither three or less nor even. The problem is that we double counted the probability of getting a 2, and the fix is to subtract out the probability of that doubly counted case.

What went wrong? If two events are not mutually exclusive, simply adding their probabilities double counts the probability of any outcome which is in both events. There is a formula for calculating or of two non-mutually exclusive events: it is called the "inclusion exclusion" principle.

Definition: Inclusion Exclusion principle

For any two events: E, F: $$ \p(E \or F) = \p(E) + \p(F) − \p(E \and F) $$

This formula does have a version for more than two events, but it gets rather complex. See the next two sections for more details.

Note that the inclusion exclusion principle also applies for mutually exclusive events. If two events are mutually exclusive $\p(E \and F) = 0$ since its not possible for both $E$ and $F$ to occur. As such the formula $\p(E) + \p(F) - \p(E \and F)$ reduces to $\p(E) + \p(F)$.

Inclusion-Exclusion with Three Events

What does the inclusion exclusion property look like if we have three events, that are not mutually exclusive, and we want to know the probability of or, $ \P(E_1 \or \E_2 \or E_3)? $

Recall that if they are mutually exclusive, we simply add the probabilities. If they are not mutually exclusive, you need to use the inclusion exclusion formula for three events:

$$ \begin{aligned} \P(E_1 &\or \E_2 \or E_3) = \\ & + \P(E_1) \\ &+ \P(E_2) \\ &+ \P(E_3) \\ & -\P(E_1 \and E_2) \\ &-\P(E_1 \and E_3) \\ &-\P(E_2 \and E_3) \\ & +\P(E_1 \and E_2 \and E_3) \end{aligned} $$

In words, to get the probability of three events, you: (1) add the probability of the events on their own. (2) Then you need to subtract off the probability of every pair of events co-occuring. (3) Finally, you add in the probability of all three events co-occuring.

Inclusion-Exclusion with $n$ Events

Before we explore the general formula, lets look at one more example. Inclusion-exclusion with four events:

$$ \begin{aligned} \P(&E_1 \or E_2 \or E_3 \or E_4) =\\ &+ \P(E_1)\\ &+ \P(E_2)\\ &+ \P(E_3)\\ &+ \P(E_4)\\ &- \P(E_1 \and E_2) \\ &- \P(E_1 \and E_3) \\ &- \P(E_1 \and E_4) \\ &- \P(E_2 \and E_3) \\ &- \P(E_2 \and E_4) \\ &- \P(E_3 \and E_4) \\ &+ \P(E_1 \and E_2 \and E_3)\\ &+ \P(E_1 \and E_2 \and E_4)\\ &+ \P(E_1 \and E_3 \and E_4)\\ &+ \P(E_2 \and E_3 \and E_4)\\ &- \P(E_1 \and E_2 \and E_3 \and E_4) \end{aligned} $$

Do you see the pattern? For $n$ events, $E_1, E_2, \dots E_n$: add all the probabilities of the events on their own. Then subtract all pairs of events. Then add all subsets of 3 events. Then subtract all subset of 4 events. Continue this process, up until subset of size $n$, adding the subsets if the size of subsets is odd, else subtracting them. The alternating addition and subtraction is where the name inclusion exclusion comes from. This is a complex process and you should first check if there is an easier way to calculate your probability. This can be written up mathematically — but it is a rather hard pattern to express in notation:

$$ \begin{gather} \P(E_1 \or E_2 \or \cdots \or E_n) = \sum\limits_{r-1}^n (-1)^{r+1} Y_r \\ \text{s.t. } Y_r = \sum\limits_{1 \leq i_1 < \cdots < i_r \leq n} \P(E_{i_1} \and \cdots \and E_{i_r}) \end{gather} $$

The notation for $Y_r$ is especially hard to parse. $Y_r$ sums over all ways of selecting a subset of $r$ events. For each selection of $r$ events, calculate the probability of the "and" of those events. $(-1)^{r+1}$ is saying: alternate between addition and subtraction, starting with addition.

It is not especially important to follow the math notation here. The main take away is that the general inclusion exclusion principle gets incredibly complex with multiple events. Often, the way to make progress in this situation is to find a way to solve your problem using another method.

The formulas for calculating the or of events that are not mutually exclusive often require calculating the probability of the and of events. Learn more in the chapter Probability of and.