Adding Random Variables

In this section on uncertainty theory we are going to explore some of the great results in probability theory. As a gentle introduction we are going to start with convolution. Convolution is a very fancy way of saying "adding" two different random variables together. The name comes from the fact that adding two random varaibles requires you to "convolve" their distribution functions. It is interesting to study in detail because (1) many natural processes can be modelled as the sum of random variables, and (2) because mathemeticians have made great progress on proving convolution theorems. For some particular random variables computing convolution has closed form equations. Importantly convolution is the sum of the random variables themselves, not the addition of the probability density functions (PDF)s that correspond to the random variables.

Adding Two Random Variables
Sum of Independent Poissons
Sum of Independent Binomials
Sum of Independent Normals
Sum of Independent Uniforms

Adding Two Random Variables

Deriving an expression for the likelihood for the sum of two random variables requires an interesting insight. If your random variables are discrete then the probability that $X + Y = n$ is the sum of mutually exclusive cases where $X$ takes on a values in the range $[0, n]$ and $Y$ takes on a value that allows the two to sum to $n$. Here are a few examples $X = 0 \and Y = n$, $X = 1 \and Y = n - 1$ etc. In fact all of the mutually exclusive cases can be enumerated in a sum:

Def: General Rule for the Convolution of Discrete Variables $$\p(X + Y = n) = \sum_{i=-\infty}^{\infty} \p(X = i, Y = n- i)$$

If the random variables are independent you can futher decompose the term $\p(X = i, Y = n- i)$. Let's expand on some of the mutually exclusive cases where $X+Y=n$:

$i$	$X$	$Y$
0	0	$n$	$\P(X=0,Y=n)$
1	1	$n-1$	$\P(X=1,Y=n-1)$
2	2	$n-2$	$\P(X=2,Y=n-2)$
	...
$n$	$n$	0	$\P(X=n,Y=0)$

Consider the sum of two independent dice. Let $X$ and $Y$ be the outcome of each dice. Here is the probability mass function for the sum $X + Y$:

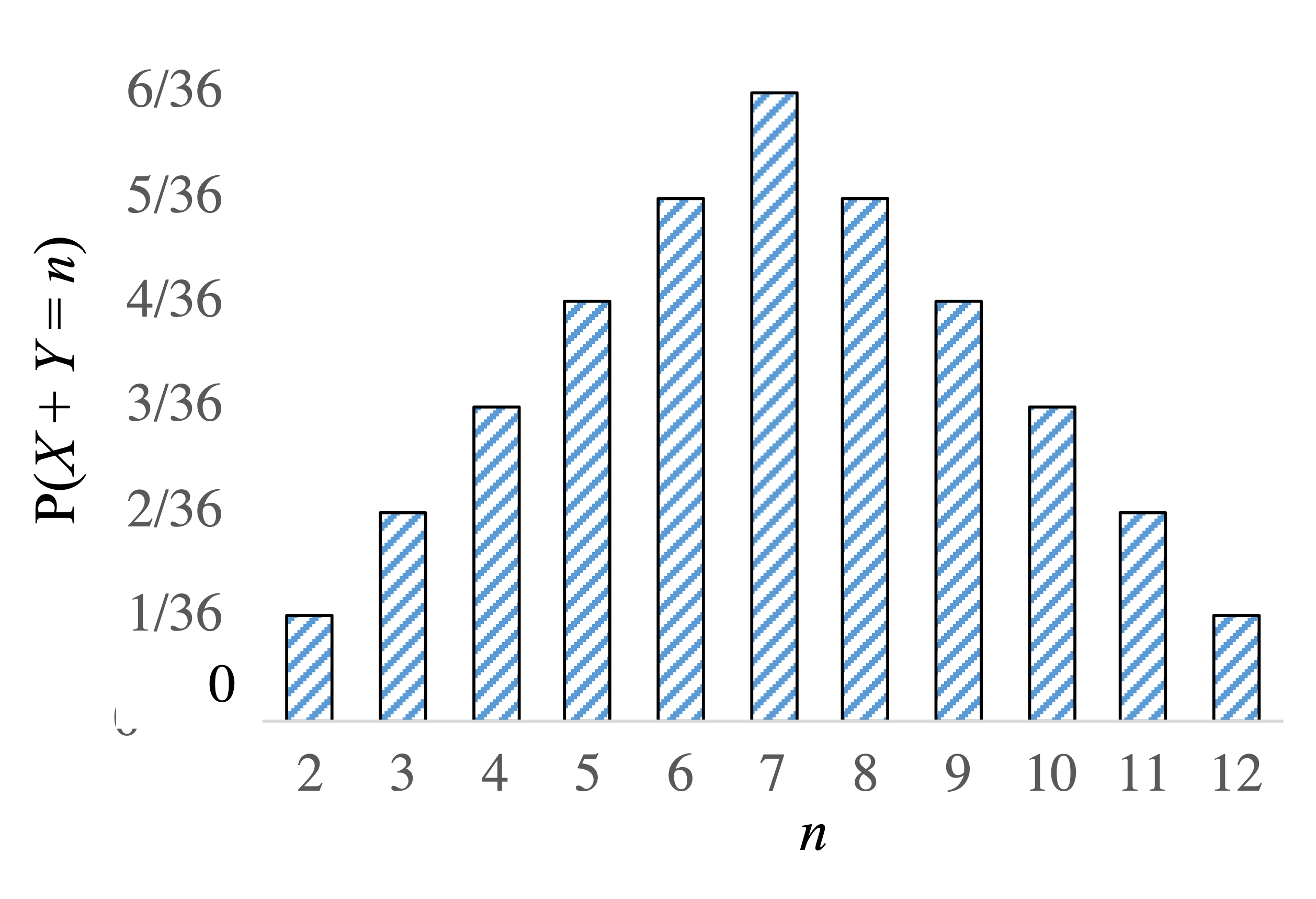
Let's use this context to practice deriving the sum of two variables, in this case $\p(X + Y = n)$, starting with the General Rule for the Convolution of Discrete Random Variables. We start by considering values of $n$ between 2 and 7. In this range $\p(X = i, Y = n- i) = \frac{1}{36}$ for all values of $i$ between 1 and $n-1$. There is exactly one outcome of the two die where $X = i$ and $Y= n-i$. For values of $i$ outside this range $n- i$ is not a valid dice outcome and $\p(X = i, Y = n- i) = 0$: \begin{align*} \p&(X + Y = n) \\ &= \sum_{i=-\infty}^{\infty} \p(X = i, Y = n- i) \\ &= \sum_{i=1}^{n-1} \p(X = i, Y = n- i) \\ &= \sum_{i=1}^{n-1} \frac{1}{36}\\ &= \frac{n-1}{36} \end{align*}

For values of $n$ greater than 7 we could use the same approach, though different values of $i$ would make $\p(X = i, Y = n- i)$ non-zero.

This derivation for a general rule has a continuous equivalent: \begin{align*} &f(X+Y = n) = \int_{i=-\infty}^{\infty} f(X = n-i, Y=i) \d i \end{align*}

Sum of Independent Poissons

For any two Poisson random variables: $X ~ \sim \Poi(\lambda_1)$ and $Y ~ \sim \Poi(\lambda_2)$ the sum of those two random variables is another Poisson: $X +Y ~ \sim \Poi(\lambda_1 + \lambda_2)$. This holds even when $\lambda_1$ is not the same as $\lambda_2$.

How could we prove a the above claim?

Example derivation:

Let's go about proving that the sum of two independent Poisson random variables is also Poisson. Let $X\sim\Poi(\lambda_1)$ and $Y\sim\Poi(\lambda_2)$ be two independent random variables, and $Z = X + Y$. What is $P(Z = n)$?

\begin{align*} P(Z = n) &= P(X + Y = n) \\ &= \sum_{k=-\infty}^{\infty} \p(X = k, Y = n- k) & \text{(Convolution)}\\ &= \sum_{k=-\infty}^{\infty} P(X = k) P(Y = n - k) & \text{(Independence)}\\ &= \sum_{k=0}^n P(X = k) P(Y = n - k) &\text{(Range of }X\text{ and }Y\text{)}\\ &= \sum_{k=0}^n e^{-{\lambda_1}} \frac{\lambda_1^k}{k!} e^{-{\lambda_2}} \frac{\lambda_2^{n-k}}{(n-k)!} & \text{(Poisson PMF)} \\ &= e^{-(\lambda_1 + \lambda_2)} \sum_{k=0}^n \frac{\lambda_1^k \lambda_2^{n-k}}{k!(n-k)!} \\ &= \frac{ e^{-(\lambda_1 + \lambda_2)}}{n!} \sum_{k=0}^n \frac{n!}{k!(n-k)!} \lambda_1^k \lambda_2^{n-k} \\ &= \frac{ e^{-(\lambda_1 + \lambda_2)}}{n!} (\lambda_1 + \lambda_2)^n & \text{(Binomial theorem)} \end{align*}

Note that the Binomial Theorem (which we did not cover in this class, but is often used in contexts like expanding polynomials) says that for two numbers $a$ and $b$ and positive integer $n$, $(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^k b^{n-k}$.

Sum of Independent Binomials with equal $p$

For any two independent Binomial random variables with the same "success" probability $p$: $X ~ \sim \Bin(n_1,p)$ and $Y ~ \sim \Bin(n_2,p)$ the sum of those two random variables is another binomial: $X +Y ~ \sim \Bin(n_1 + n_2,p)$.

This result hopefully makes sense. The convolution is the number of sucesses across $X$ and $Y$. Since each trial has the same probability of success, and there are now $n_1 + n_2$ trials, which are all independent, the convolution is simply a new Binomial. This rule does not hold when the two Binomial random variables have different parameters $p$.

Sum of Independent Normals

For any two independent normal random variables $X ~ \sim \mathcal{N}(\mu_1,\sigma_1^2)$ and $Y ~ \sim \mathcal{N}(\mu_2,\sigma_2^2)$ the sum of those two random variables is another normal: $X +Y ~ \sim \mathcal{N}(\mu_1 + \mu_2,\sigma_1^2 + \sigma_2^2)$.

Again this only holds when the two normals are independent.

Sum of Independent Uniforms

If $X$ and $Y$ are independent uniform random variables where $X \sim \Uni(0,1)$ and $Y \sim \Uni(0,1)$: \begin{align*} f(X+Y=n) = \begin{cases} n &\mbox{if } 0 < n \leq 1 \\ 2-n & \mbox{if } 1 < n \leq 2 \\ 0 & \mbox{else} \end{cases} \end{align*}

Example derivation:
Calculate the PDF of $X + Y$ for independent uniform random variables $X \sim \Uni(0,1)$ and $Y \sim \Uni(0,1)$? First plug in the equation for general convolution of independent random variables: \begin{align*} f(X+Y=n) &= \int_{i=0}^{1} f(X=n-i, Y=i)di\\ &= \int_{i=0}^{1} f(X=n-i)f(Y=i)di && \text{Independence}\\ &= \int_{i=0}^{1} f(X=n-i)di && \text{Because } f(Y=y) = 1 \end{align*} It turns out that is not the easiest thing to integrate. By trying a few different values of $n$ in the range $[0,2]$ we can observe that the PDF we are trying to calculate is discontinuous at the point $n=1$ and thus will be easier to think about as two cases: $n < 1$ and $n > 1$. If we calculate $f(X+Y=n)$ for both cases and correctly constrain the bounds of the integral we get simple closed forms for each case: \begin{align*} f(X+Y=n) = \begin{cases} n &\mbox{if } 0 < n \leq 1 \\ 2-n & \mbox{if } 1 < n \leq 2 \\ 0 & \mbox{else} \end{cases} \end{align*}