Digital Vision Test
You can find a demo of the Stanford Acuity Test here: https://myeyes.ai/. Look out for the bar icon to see the belief distribution change as the test progresses.
Digital Vision Tests
The goal of a digital vision test is to estimate how well a patient can see. You can give the patient a series of vision tests, observe their responses and then based on those responses eventually make your diagnosis. In this chapter we consider the Tumbling E tasks. The patient is presented an E at a chosen font size. The E will be randomly written up, down, left or right and the patient must say which direction it is facing. Their guess will either be correct, or incorrect. The patient will have a series of 20 of these tasks. Vision tests as useful for people who need glasses, but can be critical for folks with eye disease who need to closely monitor for subtle decreases in vision.
There are two primary tasks in a digital vision test: (1) based on the patient responses, infer their ability to see and (2) select the next font size to show to the patient.
How to Represent Ability to See?
Ability is a random variable! We define $A$ to represent the ability of someone to see. $A$ takes on values between 0.0 (representing legal blindness) and 1.0 (representing standard vision). While ability to see is in theory a continuous random variable, we are going to represent ability to see as discretized into one hundreths. As such $A \in \{0.00, 0.01, \dots, 0.99\}$. As a small aside, visual acuity can be represented in many different units (such as a log based unit called LogMAR). We chose this 0 to 1 scale as it makes the math easier to explain.
The prior probability mass function for $A$, written as $\p(A=a)$, represents our belief that $A$ takes on the value of $a$, before we have seen any observations about the patient. This prior belief comes from the natural distribution of how well people can see. To make our algorithm most accurate, the prior should best reflect our patient population. Since our eye test is built for doctors in an eye hospital, we used historical data from eye hospital visits to build our prior. Here is $P(A=a)$ as a graph:
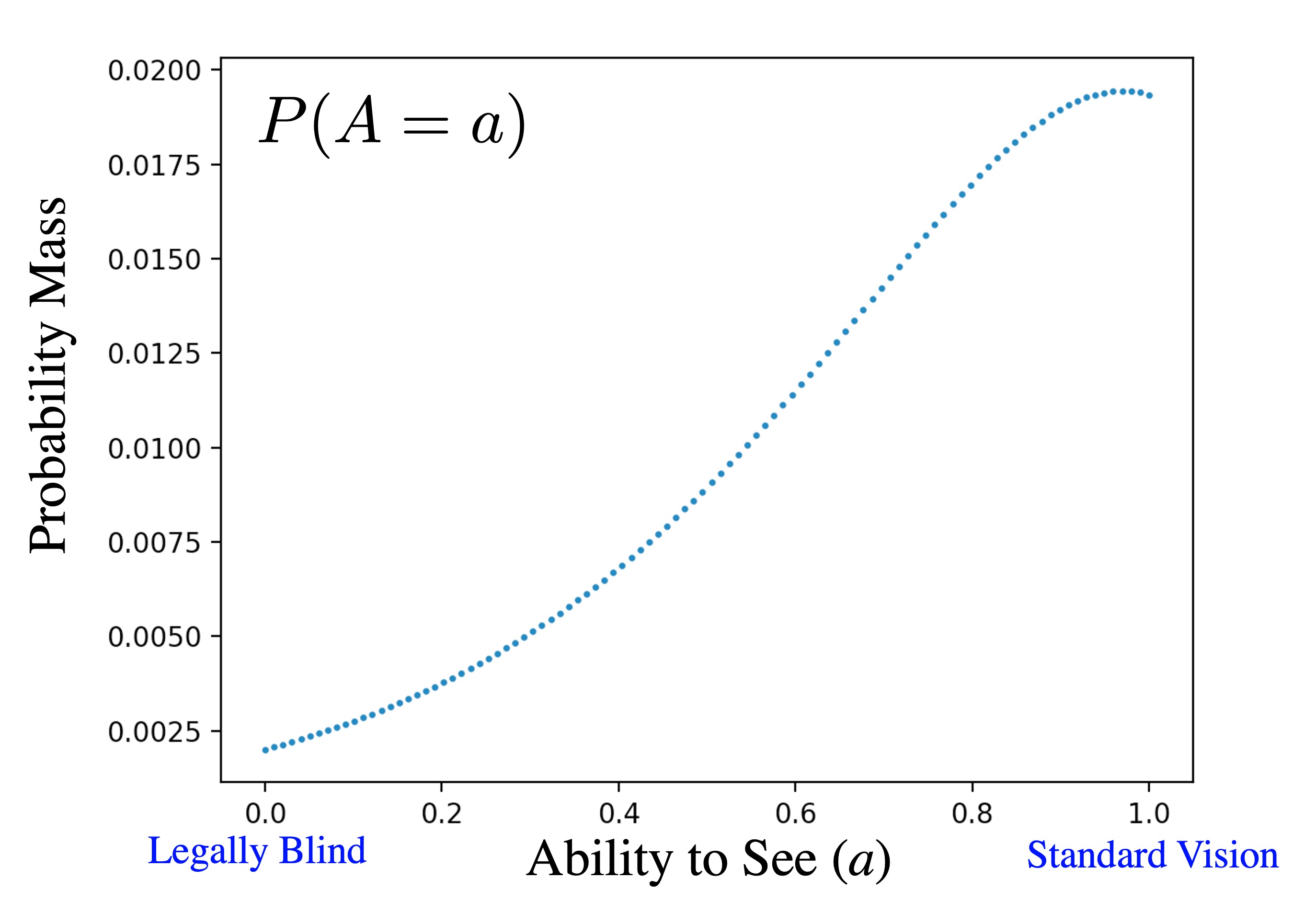
The prior belief on ability to see
Here is that exact same probability mass function written as a table. A table representation is possible because of our choice to discretize $A$. In code we can access $\p(A=a)$ as a dictionary lookup, belief[a] where belief stores the whole probability mass function:
| $a$ | $\P(A=a)$ | $a$ | $\P(A=a)$ | $a$ | $\P(A=a)$ | ||
| 0.00 | 0.0020 | 0.20 | 0.0037 | $\cdots$ | |||
| 0.01 | 0.0021 | 0.21 | 0.0038 | 0.81 | 0.0171 | ||
| 0.02 | 0.0021 | 0.22 | 0.0040 | 0.82 | 0.0173 | ||
| 0.03 | 0.0022 | 0.23 | 0.0041 | 0.83 | 0.0175 | ||
| 0.04 | 0.0023 | 0.24 | 0.0042 | 0.84 | 0.0177 | ||
| 0.05 | 0.0023 | 0.25 | 0.0043 | 0.85 | 0.0180 | ||
| 0.06 | 0.0024 | 0.26 | 0.0045 | 0.86 | 0.0181 | ||
| 0.07 | 0.0025 | 0.27 | 0.0046 | 0.87 | 0.0183 | ||
| 0.08 | 0.0026 | 0.28 | 0.0048 | 0.88 | 0.0185 | ||
| 0.09 | 0.0026 | 0.29 | 0.0049 | 0.89 | 0.0186 | ||
| 0.10 | 0.0027 | 0.30 | 0.0050 | 0.90 | 0.0188 | ||
| 0.11 | 0.0028 | 0.31 | 0.0052 | 0.91 | 0.0189 | ||
| 0.12 | 0.0029 | 0.32 | 0.0054 | 0.92 | 0.0190 | ||
| 0.13 | 0.0030 | 0.33 | 0.0055 | 0.93 | 0.0191 | ||
| 0.14 | 0.0031 | 0.34 | 0.0057 | 0.94 | 0.0192 | ||
| 0.15 | 0.0032 | 0.35 | 0.0058 | 0.95 | 0.0192 | ||
| 0.16 | 0.0033 | 0.36 | 0.0060 | 0.96 | 0.0192 | ||
| 0.17 | 0.0034 | 0.37 | 0.0062 | 0.97 | 0.0193 | ||
| 0.18 | 0.0035 | 0.38 | 0.0064 | 0.98 | 0.0192 | ||
| 0.19 | 0.0036 | 0.39 | 0.0066 | 0.99 | 0.0192 | ||
Observations
Once the patient starts the test, you will begin collecting observations. Consider this first observation, $\text{obs}_1$ where the patient was shown a letter with font size 0.7 and answered the question incorrectly:
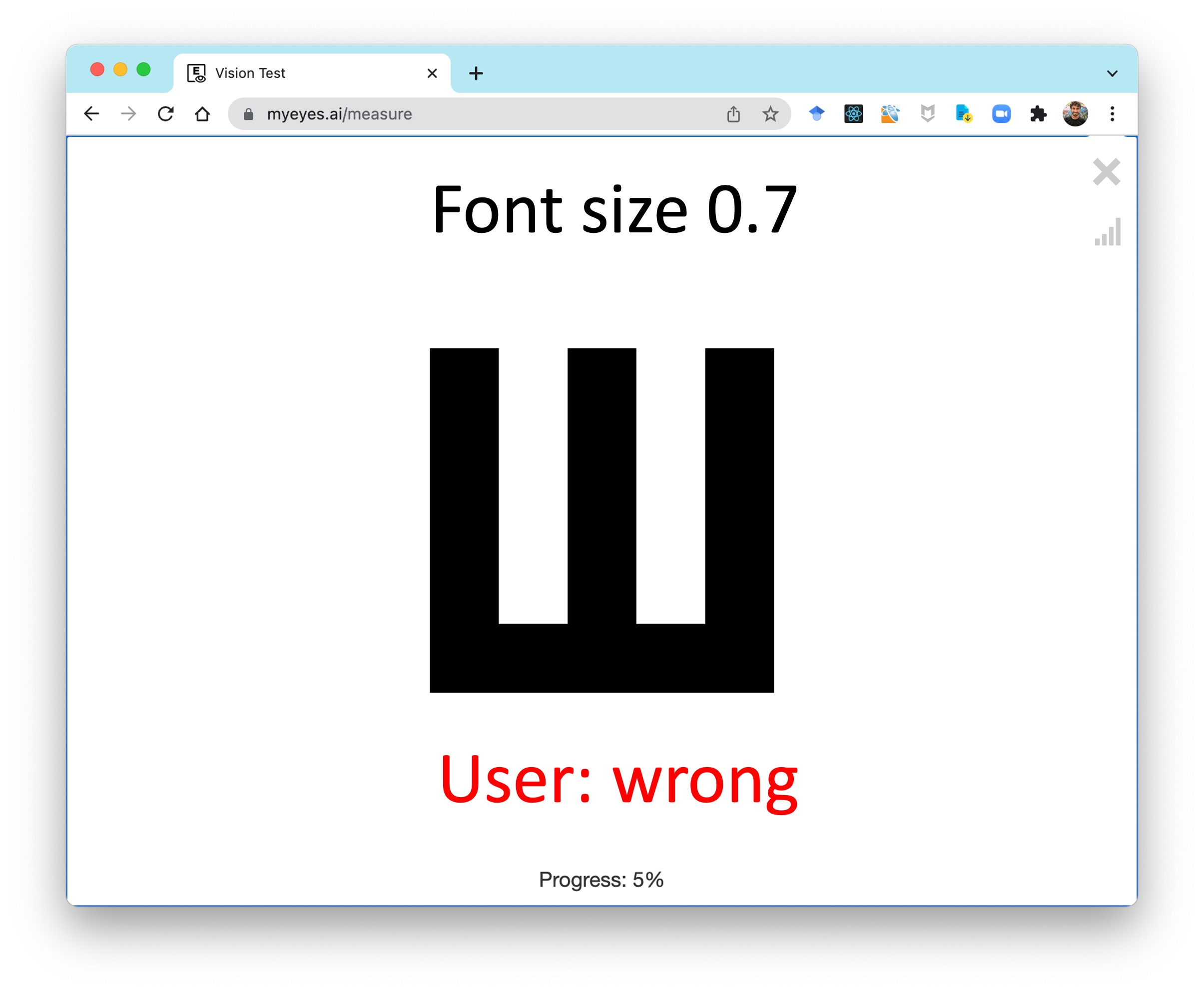
We can represent this observation as a tuple with font size and correctness. Mathematically this could be written as $\text{obs}_1 = [0.7, \text{False}]$. In code this observation could be stored as a dictionary
obs_1 = {
"font_size":0.7,
"is_correct":False
}Eventually we will have 20 of these observations: $[\text{obs}_1, \text{obs}_2, \dots, \text{obs}_{20}]$.
Infering Ability
Our first major task is to write code which can update our probability mass function for $A$ based on observations. First let us consider how to update our belief in ability to see from a single observation, $\text{obs}$ (aside: formally this the event that random variable $\text{Obs}$ takes on the value $\text{obs}$). We can use Bayes' Theory for random variables:
\begin{align*}
\P(A=a|\text{obs}) &= \frac{\P(\text{obs}|A=a)P(A=a)}{\P(\text{obs})}\end{align*}
This will be computed inside a for loop for each assignment $a$ to ability to see. How can we compute each term in the Bayes' Theorem expression? We already have values for the prior $\p(A=a)$ and we can compute the denominator $\p(\text{obs})$ using the Law of Total Probability:
\begin{align*}
\P(\text{obs}) &= \sum_x \P(\text{obs}, A=x) && \href{ ../../part1/law_total/}{\text{LOTP}} \\
&= \sum_x P(\text{obs} | A=x)P(A=x)&&\text{Chain Rule}
\end{align*}
Notice how the terms in this new expression for $\p(\text{obs})$ already show up in the numerator of our Bayes' Theorem equation. As such, in code we are going to (1) compute the numerator for every value of $a$, store it as the value of belief, (2) compute the sum of all of those terms and (3) devide each value of belief by the sum. The process of doing steps 2 and 3 is also known as normalization:
def update_belief(belief, obs):
"""
Take in a prior belief (stored as a dictionary) for a random
variable representing how well someone can see based on a single
observation (obs). Update the belief based using Bayes' Theorem
"""
# loop over every value in the support of the belief RV
for a in belief:
# the prior belief P(A = a)
prior_a = belief[a]
# the obs probability P(obs | A = a)
likelihood = calc_likelihood(a, obs)
# numerator of Bayes' Theorem
belief[a] = prior_a * likelihood
# calculate the denominator of Bayes' Theorem
normalize(belief)
def normalize(belief):
# in place normalization of a belief dictionary
total = belief_sum(belief)
for key in belief:
belief[key] /= total
def belief_sum(belief):
# get the sum of probability mass for a discrete belief
total = 0
for key in belief:
total += belief[key]
return totalAt this point we have an expression, and corresponding code, to update our belief in ability to see given an observation. However we are missing a way to compute $\p(\text{obs}|A=a)$. In our code this expression is the currently undefined calc_likelihood(a, obs) function. In the next section we will go over how to compute this "likelihood" function. Before we do so, let's take a look at the result of applying update_belief for a patient with the single observation obs_1 defined above.
obs_1 says that this patient got a rather large letter (font-size of 0.7) incorrect. As such in our posterior we think they can't see very well, though we have a lot of uncertainty as it has only been one observation. This belief is expressed in our updated probability mass function for $A$, $\p(A = a | \text{obs}_1)$, called the posterior. Here is what the posterior looks like for obs_1. Note that the posterior $\p(A=a|\text{obs}_1)$ is still represented in code as a dictionary, as in the prior, $\p(A=a)$:
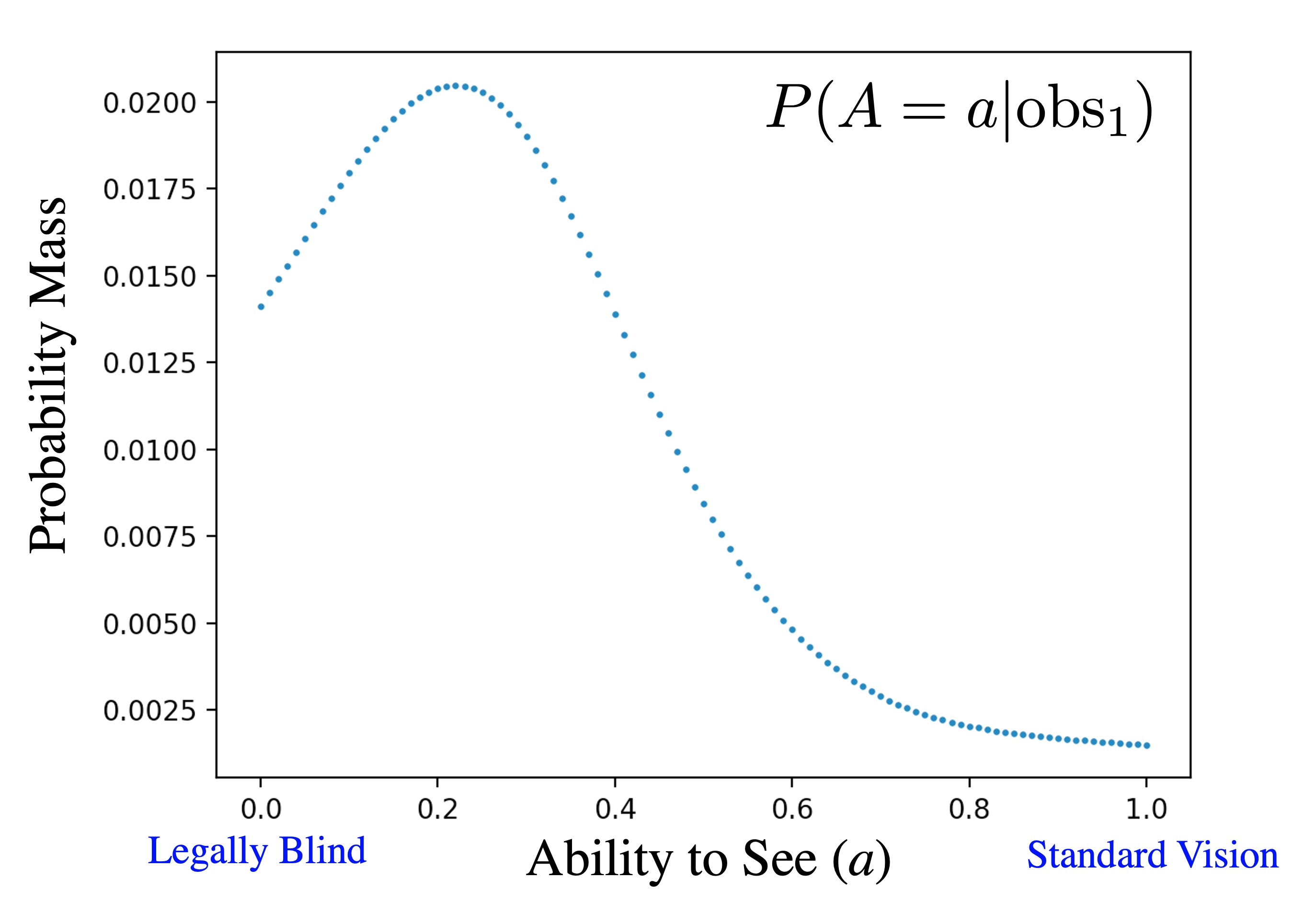
The posterior belief on ability to see given a patient incorrectly identified a letter with font size 0.7. It shows a belief that the patient can't see very well.
Likelihood Function
We are not done yet! We have not yet said how we will compute $\p(\text{obs}|A=a)$. In Bayes' Theorem this term is called the "likelihood." The likelhood for our eye exam will be function that returns back probabilities for inputs of $a$ and $\text{obs}$. In python this will be a function calc_likelihood(a, obs). In this function obs is a single observation such as obs_1 described above. Imagine a concrete call to the likelihood function bellow. This call will return back the probability a person who has true ability to see of 0.5 would get a letter of font-size 0.7 incorrect.
# get an observation
obs = {
"font_size":0.7,
"is_correct":False
}
# calculate likelihood for obs given a, P(obs | A = a)
calc_likelihood(a = 0.5, obs)Note 1: When computing the likelihood term, $\p(\text{obs}|A=a)$, we do not have to estimate $A$ as it shows up on the right hand size of the conditional. In the likelihood term we are told exactly how well the person can see. Their vision is truly $a$. Do not be fooled by the fact that $a$ is a (non-random) variable. When computing the likelihood function this varaible will have a numeric value.
Note 2: The variable obs represents a single patient interaction. It has two parts: a font-size and a boolean for whether the patient got the letter correct. However, we don't think of font-size as being a random variable. Instead we think of it as a contant which has been fixed by the computer. As such $\p(\text{obs}|A=a)$ can be simplified to $\p(\text{correct}|A=a)$. "correct" is short hand for the event that a random variable Correct takes on the True or False value correct:
\begin{align*}
\p(&\text{obs}|A=a) \\
&= \p(\text{correct}, f|A=a) && \text{obs is a tuple} \\
&= \p(\text{correct}|A=a) && f \text{ is a constant }
\end{align*}
Defining the likelihood function $\p(\text{correct}|A=a)$ involves more medical and education theory than probability theory. You don't need to know either for this course! But it is still neat to learn and without the likelihood function we won't have complete code. So, let's dive in.
A very practical starting point for the likelihood function for a vision test comes from a classic education model called "Item Response Theory", also known as IRT. IRT assumes the probability that a student with ability $a$ gets a question with difficulty $d$ correct is governed by the easy to compute function: \begin{align*} \p(&\text{Correct} = \text{True}|a) \\ &= \text{sigmoid}(a-d) && d \text{ is difficulty} \\ &= \frac{1}{1+e^{-(a-d)}} \\ \end{align*} where $e$ is the natural base constant and $\text{sigmoid}(x) = \frac{1}{1+e^{-x}}$. The sigmoid function is a handy function which takes in any real valued input and returns a corresponding value in the range $[0, 1]$.
This IRT model introduces a new constant: difficulty of a letter $d$. How difficult is it to correctly respond to a letter with a given font size? The simplest way to model difficulty, while accounting for the fact that large font sizes are easier than small ones, is to define the difficulty of a letter with font size $f$ to be $d = 1-f$. Plugging this in: \begin{align*} \p(&\text{Correct} = \text{True}|a)\\ &= \text{sigmoid}(a-[1-f])\\ &= \text{sigmoid}(a-1+f)\\ &= \frac{1}{1+e^{-(a-1+f)}} \end{align*} We now have a complete, if simplistic, liklihood function! In code it would look like this:
def calc_likelihood(a, obs):
# returns P(obs | A = a) using Item Response Theory
f = obs["font_size"]
p_correct_true = sigmoid(a + f - 1)
if obs["is_correct"]:
return p_correct_true
else:
return 1 - p_correct_true
def sigmoid(x):
# the classic squashing function. All outputs are [0,1]
return 1 / (1 + math.exp(-x))
In the published version of the Stanford Acuity Test we extend Item Response Theory in several ways. We have a term for the probability that a patient gets the answer correct by random guessing as well as a term that they make a mistake, aka "slip", even though they know the correct answer. We also observed that a Floored Exponential seems to be a more accurate function than the sigmoid. These extensions are beyond the scope of this chapter as they are not central to the probability insight. For more details see the original paper [1].
Multiple Observations
What if you have multiple observations? For multiple observations the only term that will change will be the likelihood term $\p(\text{Observations}|A=a)$. We assume that each observation is independent, conditioned on ability to see. Formally $$\p(\text{obs}_1, \dots, \text{obs}_{20} |A=a) = \prod_i \p(\text{obs}_i|A=a)$$ As such the likelihood of all observations will be the product of the likelihood of each observation on its own. This is equivalent mathematically to calculating the posterior for one observation and calling the posterior your new prior.
The Full Code
Here is the full code for inference of ability to see given observations, minus the user interface functions and the file reading for the prior belief:
def main():
"""
Compute your belief in how well someone can see based
off an eye exam with 20 questions at different fonts
"""
belief_a = load_prior_from_file()
observations = get_observations()
for obs in observations:
update_belief(belief_a,obs)
plot(belief_a)
def update_belief(belief, obs):
"""
Take in a prior belief (stored as a dictionary) for a random
variable representing how well someone can see based on a single
observation (obs). Update the belief based using Bayes' Theorem
"""
# loop over every value in the support of the belief RV
for a in belief:
# the prior belief P(A = a)
prior_a = belief[a]
# the obs probability P( obs | A = a)
likelihood = calc_likelihood(a, obs)
# numerator of Bayes' Theorem
belief[a] = prior_a * likelihood
# calculate the denominator of Bayes' Theorem
normalize(belief)
def calc_likelihood(a, obs):
# returns P(obs | A = a) using Item Response Theory
f = obs["font_size"]
p_correct = sigmoid(a + f - 1)
if obs["is_correct"]:
return p_correct
else:
return 1 - p_correct
# ----------- Helper Functions -----------
def sigmoid(x):
# the classic squashing function. All outputs are [0,1]
return 1 / (1 + math.exp(-x))
def normalize(belief):
# in place normalization of a belief dictionary
total = belief_sum(belief)
for key in belief:
belief[key] /= total
def belief_sum(belief):
# get the sum of probability mass for a discrete belief
total = 0
for key in belief:
total += belief[key]
return totalChosing the Next Font Size
At this point, we have a way to calculate a probability mass function of our belief in how well the patient can see, at any point in our test. This leaves one more task for us to perform: In a digital eye test, we select the next font size to show to the patient. Instead of showing a predetermined set, we should make a choice which is informed by our current belief in how well the patient can see. We were inspired by Thompson Sampling, an algorithm which is able to balance exploring uncertainty and narrowing in on your most confident belief. When chosing a font size we simply take a sample from our current belief $A$ and then chose the font size that we think a person with ability with that sampled value could see with 80% accuracy. We chose the 80% constant so that the eye test would not be too painful.
One of the neat take aways from this application is that there are many problems where you could take the knowledge learned from this course and improve on the current state of the art! Often the most creative task is to recognize where computer based probability could be usefully applied. Even for eye tests this is not the end of the story. The Stanford Eye Test, which started in CS109, is just a step on the journey to a more accurate digital eye test. There is ./always a better way. Have an idea?
Publications and press coverage:
| [1] | The Stanford Acuity Test: A Precise Vision Test Using Bayesian Techniques and a Discovery in Human Visual Response. Association for the Advancement of Artificial Intelligence |
| [2] | Digitising the vision test. The Lancet Journal. |
| [3] | Eye, robot: Artificial intelligence dramatically improves accuracy of classic eye exam. Science Magazine. |