$\DeclareMathOperator{\p}{P}$ $\DeclareMathOperator{\P}{P}$ $\DeclareMathOperator{\c}{^C}$ $\DeclareMathOperator{\or}{ or}$ $\DeclareMathOperator{\and}{ and}$ $\DeclareMathOperator{\var}{Var}$ $\DeclareMathOperator{\Var}{Var}$ $\DeclareMathOperator{\Std}{Std}$ $\DeclareMathOperator{\E}{E}$ $\DeclareMathOperator{\std}{Std}$ $\DeclareMathOperator{\Ber}{Bern}$ $\DeclareMathOperator{\Bin}{Bin}$ $\DeclareMathOperator{\Poi}{Poi}$ $\DeclareMathOperator{\Uni}{Uni}$ $\DeclareMathOperator{\Geo}{Geo}$ $\DeclareMathOperator{\NegBin}{NegBin}$ $\DeclareMathOperator{\Beta}{Beta}$ $\DeclareMathOperator{\Exp}{Exp}$ $\DeclareMathOperator{\N}{N}$ $\DeclareMathOperator{\R}{\mathbb{R}}$ $\DeclareMathOperator*{\argmax}{arg\,max}$ $\newcommand{\d}{\, d}$

Law of Total Probability

An astute person once observed that when looking at a picture, like the one we saw for conditional probability:

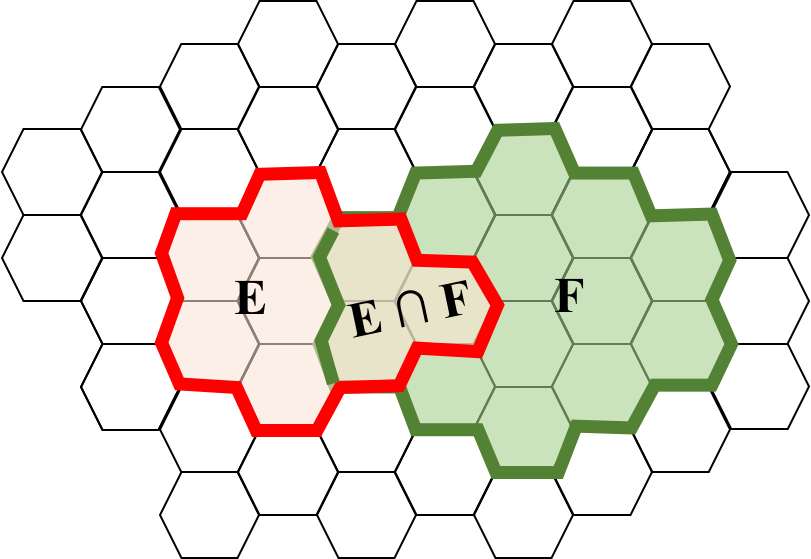
that event $E$ can be thought of as having two parts, the part that is in $F$, $(E \and F)$, and the part that isn’t, $(E \and F\c)$. This is true because $F$ and $F\c$ are (a) mutually exclusive sets of outcomes which (b) together cover the entire sample space. After further investigation this proved to be mathematically true, and there was much rejoicing:

$$ \begin{align} \p(E) &= \p(E \and F) + \p(E \and F\c) \end{align} $$

This observation proved to be particularly useful when it was combined with the chain rule and gave rise to a tool so useful, it was given the big name, law of total probability: $$ \begin{align} \p(E) &= \p(E \and F) + \p(E \and F\c) \\ &= \p(E | F) \p(F) + \p(E | F\c) \p(F\c) \\ \end{align} $$

The Law of Total Probability (LOTP)
If we combine our above observation with the chain rule, we get a very useful formula the Law of Total Probability of LOTP for short: $$ \begin{align} \p(E) &= \p(E | F) \p(F) + \p(E | F\c) \p(F\c) \end{align} $$

There is a more general version of the rule. If you can divide your sample space into any number of mutually exclusive events: $B_1, B_2, \dots B_n$ such that every outcome in the sample space falls into one of those events, then: $$ \begin{align} \p(E) &= \sum_{i=1}^n \p(E \and B_i) && \text{Extension of our observation}\\ &= \sum_{i=1}^n \p(E | B_i) \p(B_i) && \text{Using chain rule on each term} \end{align} $$

Generalization to Many Background Events

The events $F$ and $F^C$ are always mutually exclusive and they always cover the entire sample space, no matter what $F$ represents! If you can find more than two background events that are also mutually exclusive, and their union covers the entire sample space (the universe of outcomes) then you can use the generalized version of the law of total probability.

To generalize the law of total probability, imagine we can divide the sample space into several mutually exclusive background events $( B_1, B_2, \dots, B_n )$, where these sets cover the entire sample space. In this case, any event $E$ can be decomposed by considering the likelihood of $E$ within each of these disjoint sets.

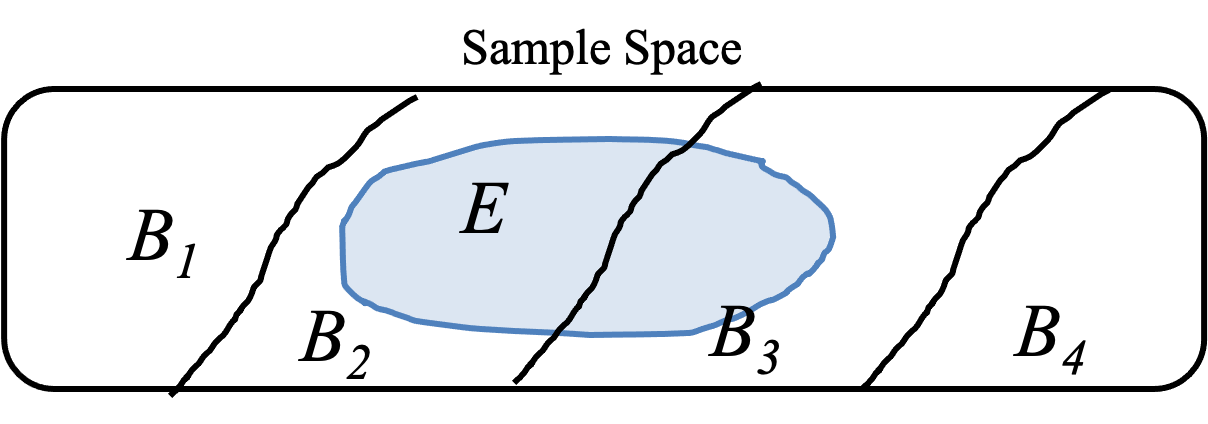
In the image above, you could compute $\p(E)$ to be equal to $$\p\Big[(E \and B_1) \text{ }\or \text{ }(E \and B_2)\text{ } \or \text{ } \dots \text{ } \or \text{ }(E \and B_n)\big]$$ There are many real world cases where (a) it is much easier to think of the probability of an event $E$ in the context of a background event $B_i$ and the sample space can be discretized into several mutual exclusive background events $B_i$. Lets start with an example with three events $B_1, B_2, B_3$. Suppose you are trying to determine the likelihood that a randomly selected individual will test positive for a certain disease, $\p(E)$. The population can be divided into three mutually exclusive groups :

  1. $B_1$: Individuals who are high-risk (e.g., individuals with a known exposure to the disease),
  2. $B_2$: Individuals who are medium-risk (e.g., individuals with a family history of the disease but no direct exposure),
  3. $B_3$: Individuals who are low-risk (e.g., the general population without known risk factors).
Each of these groups has a different probability of testing positive for the disease, and the total probability of a random individual testing positive can be broken down as follows: $$ \begin{align} \P(E) &= \P(E \and B_1) + \P(E \and B_2) + \P(E \and B_3) && \text{LOTP}\\ &= \P(E | B_1)P(B_1) + \P(E | B_2)P(B_2) + \P(E | B_3)P(B_3) && \text{Chain Rule}\\ &= \sum_{i=1}^{3} P(E \mid B_i)P(B_i) && \text{Sum Notation} \end{align} $$

Where:

  • $P(E | B_1)$ is the probability of testing positive given someone in the high-risk group
  • $P(E | B_2)$ is the probability of testing positive given someone in the medium-risk groups,
  • $P(E | B_3)$ is the probability of testing positive given a person is in the low-risk group.
  • $ P(B_1)$, $P(B_2)$ and $P(B_3)$ are the probabilities of a person being in the high-risk, medium-risk and low-risk groups.

This works because everyone can belongs to one of the background events ($B_1, B_2, B_3$), in other words the sets span the sample space. Moreovoer each person is in only one of the sets, and as such they are mututally exclusive. It is helpful because its easier to think of the probability of $E$, testing positive, in the context of the background events, where you know how at risk the patient is.